A tutorial on binary descriptors – part 3 – The ORB descriptor

38 Replies

This third post in our series about binary descriptors that will talk about the ORB descriptor [1]. We had an introduction to patch descriptors, an introduction to binary descriptors and a post about the BRIEF [2] descriptor.

We’ll start by showing the following figure that shows an example of using ORB to match between real world images with viewpoint change. Green lines are valid matches, red circles indicate unmatched points.

ORB descriptor - An example of keypoints matching using ORB

ORB descriptor – An example of keypoints matching using ORB

Now, as you may recall from the previous posts, a binary descriptor is composed out of three parts:

  1. A sampling pattern: where to sample points in the region around the descriptor.
  2. Orientation compensation: some mechanism to measure the orientation of the keypoint and rotate it to compensate for rotation changes.
  3. Sampling pairs: the pairs to compare when building the final descriptor.

Recall that to build the binary string representing a region around a keypoint we need to go over all the pairs and for each pair (p1, p2) – if the intensity at point p1 is greater than the intensity at point p2, we write 1 in the binary string and 0 otherwise.

The ORB descriptor is a bit similar to BRIEF. It doesn’t have an elaborate sampling pattern as BRISK [3] or FREAK [4]. However, there are two main differences between ORB and BRIEF:

  1. ORB uses an orientation compensation mechanism, making it rotation invariant.
  2. ORB learns the optimal sampling pairs, whereas BRIEF uses randomly chosen sampling pairs.

Orientation Compensation

ORB uses a simple measure of corner orientation – the intensity centroid [5]. First, the moments of a patch are defined as:

ORB descriptor-Patch's moments definition

ORB descriptor-Patch’s moments definition

With these moments we can find the centroid, the “center of mass” of the patch as:

ORB descriptor - Center of mass of the patch

ORB descriptor – Center of mass of the patch

We can construct a vector from the corner’s center O, to the centroid -OC. The orientation of the patch is then given by:

ORB descriptor - Orientation of the patch

ORB descriptor – Orientation of the patch

Here is an illustration to help explain the method:

ORB descriptor - Angle calculation illustration

ORB descriptor – Angle calculation illustration

Once we’ve calculated the orientation of the patch, we can rotate it to a canonical rotation and then compute the descriptor, thus obtaining some rotation invariance.

Learning the sampling pairs

There are two properties we would like our sampling pairs to have. One is uncorrelation – we would like that the sampling pairs will be uncorrelated so that each new pair will bring new information to the descriptor, thus maximizing the amount of information the descriptor carries. The other is high variance of the pairs – high variance makes a feature more discriminative, since it responds differently to inputs.

The authors of ORB suggest learning the sampling pairs to ensure they have these two properties. A simple calculation [1] shows that there are about 205,000 possible tests (sampling pairs) to consider. From that vast amount of tests, only 256 tests will be chosen.

The learning is done as follows. First, they set a training set of about 300,000 keypoints drawn from the PASCAL 2006 dataset [6].Next, we apply the following greedy algorithm:

  1. Run each test against all training patches.
  2. Order the tests by their distance from a mean of 0.5, forming the vector T.
  3. Greedy search:
    1. Put the first test into the result vector R and remove it from T.
    2. Take the next test from T, and compare it against all tests in R. If its absolute correlation is greater than a threshold, discard it; else, add it to R.
    3. Repeat the previous step until there are 256 tests in R. If there are fewer than 256, raise the threshold and try again.

Once this algorithm terminates, we obtain a set of 256 relatively uncorrelated tests with high variance.

To conclude, ORB is binary descriptor that is similar to BRIEF, with the added advantages of rotation invariance and learned sampling pairs. You’re probably asking yourself, how does ORB perform in comparison to BRIEF? Well, in non-geometric transformation (those that are image capture dependent and do not rely on the viewpoint, such as blur, JPEG compression, exposure and illumination) BRIEF actually outperforms ORB. In affine transformation, BRIEF perform poorly under large rotation or scale change as it’s not designed to handle such changes. In perspective transformations, which are the result of view-point change, BRIEF surprisingly slightly outperforms ORB. For further details, refer to [7] or wait for the last post in this tutorial which will give a performance evaluation of the binary descriptors.

The next post will talk about BRISK [3] that was actually presented in the same conference as ORB. It presents some difference from BRIEF and ORB by using a hand-crafted sampling pattern.

Gil.

References:

[1] Rublee, Ethan, et al. “ORB: an efficient alternative to SIFT or SURF.” Computer Vision (ICCV), 2011 IEEE International Conference on. IEEE, 2011.‏

[2] Calonder, Michael, et al. “Brief: Binary robust independent elementary features.” Computer Vision–ECCV 2010. Springer Berlin Heidelberg, 2010. 778-792.‏

[3] Leutenegger, Stefan, Margarita Chli, and Roland Y. Siegwart. “BRISK: Binary robust invariant scalable keypoints.” Computer Vision (ICCV), 2011 IEEE International Conference on. IEEE, 2011.‏

[4] Alahi, Alexandre, Raphael Ortiz, and Pierre Vandergheynst. “Freak: Fast retina keypoint.” Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on. IEEE, 2012.‏

[5] Rosin, Paul L. “Measuring corner properties.” Computer Vision and Image Understanding 73.2 (1999): 291-307.‏

[6] M. Everingham. The PASCAL Visual Object Classes Challenge 2006 (VOC2006) Results. http://pascallin.ecs.soton.ac.uk/challenges/VOC/databases.html.

[7] Heinly, Jared, Enrique Dunn, and Jan-Michael Frahm. “Comparative evaluation of binary features.” Computer Vision–ECCV 2012. Springer Berlin Heidelberg, 2012. 759-773.‏

38 thoughts on “A tutorial on binary descriptors – part 3 – The ORB descriptor”

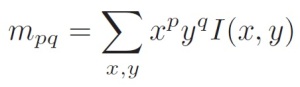
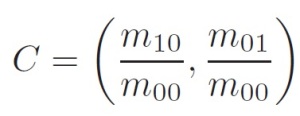
  1. Pingback: A tutorial on binary descriptors – part 4 – The BRISK descriptor | Gil's CV blog

  2. Pingback: A tutorial on binary descriptors – part 5 – The FREAK descriptor | Gil's CV blog

  3. Alex

    I cannot thank you enough for these wonderfully written tutorials! A thing of beauty, that’s what they are! I’m currently writing my bachelor thesis on generation of ortho-maps using UAVs. For the stitching of the aerial photos together I chose a feature-based apporoach (detecting features, calculating homographies, using bundle adjustement to align them together etc.) with ORB. However the documention provide in the OpenCV docs is so bad that it almost made me cry. Alone the tutorials are usually in the form of an introduction (couple of sentences that you can read in Wikipedia), a bunch of code and images where the result is shown. The “Explanation” part is in 99% of the cases left empty. Still trying to figure out how exactly the descriptor vector for a keypoint is built in OpenCV (32 integer values :D) but will get to it soon. Your tutorials have been a incredible help and again I’d like to thank you from the bottom of my heart. You are a good man indeed.

    Reply ↓
    1. gillevicv Post author

      Thank you for your kind words.

      If you’d like, I can try to help you with the OpenCV implementation (for example, it’s fairly simple understanding why it’s 32 integer values).

      Mail me at gil.levi100@gmail.com if you’re interested.

      Gil.

      Reply ↓
      1. Alex

        No problem, man. Thanks for the offer. I like to leave some work for my own brain in all this 😀 As for the 32 integer values I know why they are 32 in a single descriptor (the matrix dimensions are n*32 with n = number of keypoints in the image the descriptor set belongs to). The only thing I’m currently still figuring out is how they are put in there. All of them are 8 bit values (0-255) which is like intensity value (since we have grayscale images). ORB uses BRIEF-32 (32 bytes * 8 = 256 bit string). As you can see i’m pretty close. The problem is that the sources of OpenCV don’t tell much and you have to dig a lot. At least the ORB paper is decent enough to get me going. Currently reading it. :3 It mentions about the 5×5 patches in 31×31 sub-windows for each keypoint. Just have to visualize it, that’s all. I’d like to make some pretty diagrams so that I can explain things in such a way that people without much knowledge in those things can actually understand it. Like you did in those tutorials. Thanks again for your awesome work!

  4. Virat

    Wow! Thanks a lot for coming up with this blog. Its been tremendous help for me to write my thesis.I could find no video lectures nor any sort of explanations anywhere else in the internet.Thank you once again.

    Reply ↓
  5. changkai

    Hi Nice BLOG~
    I plan to use ORB to implement a AR application on mobile device. Is that possible ORB will match the requirements of robust and speed ? If not , are there any other options?
    SIFT and SURF are too slow for AR app on mobile device, so I aim to BRISK or ORB but I am sort of confused which is the best?

    Reply ↓

  6. Pingback: Adding rotation invariance to the BRIEF descriptor | Gil's CV blog

  7. Pingback: Performance Evaluation of Binary Descriptor – Introducing the LATCH descriptor | Gil's CV blog

  9. dashesi

    hi ,for my final year project, i need to implement ORB .I need your help, ideas , how to proceed and so on

    Reply ↓
    1. gillevicv Post author

      Hi,

      Thank you for your interest in my blog.

      I would suggest to go over the paper and take a look at OpenCV’s implementation.

      Best,
      Gil

      Reply ↓
  10. cipritom

    Hi! Thank you for these amazing tutorials! They’re gold!
    I’ve just read the paper of ORB and I’m a bit confused regarding ‘steered’ BRIEF. I understand that ‘steering’ doesn’t work: “Steered BRIEF has signif­icantly lower variance, however, since the eigenvalues are lower, and thus is not as discriminative”.
    So do they still use this ?

    Reply ↓
  11. WhoAmI

    Am a novie to this field of image recognition and I came through your blog and started learning from here by reading your tutorials on Feature Point detectors and descriptors. I have a question on ORB.

    Is it possible to use Gaussian filters with ORB to get much better results for Image recognition?

    Reply ↓
    1. gillevicv Post author

      Hi,

      Thanks you for your interest in my blog.

      What do you mean by “using Gaussian filters with ORB”? In ORB (and some of the other descriptors), in every sampling pair, the two pixels that are compared undergo a certain Gaussian blur before the comparison.

      Gil.

      Reply ↓
  12. Rajdeep

    Is ORB implemented in matlab. if yes then please help me in coding. or if it is not implemented using matlab then reply me in which software it is implemented and if you have code then please mail me. I have urgent need of this code.

    Reply ↓
  13. John

    Hey Gil,

    I came to know that ORB uses Harris Cornerness measure and scale pyramid to FAST detector. I used ORB in my code (Java) as below

    FeatureDetector mFeatureDetector = FeatureDetector.create(FeatureDetector.ORB);

    Does this by default uses Harris Corner to find corners in an image and scale pyramid or else I need to code harris corner too? How much is the point of scale pyramid in ORB?

    Reply ↓
  14. Ledig

    I was just reading the official paper of ORB from Ethan Rublee and somewhat I find hard to understand the section of “4.3 Learning Good Binary Features”

    I was surfing over the Internet to dig much deep into it and I found the below paragraph. I haven’t getting the practical explanation of this. Can any of you explain me this in a simple terms.

    “Given a local image patch in size of m × m, and suppose the local window (i.e., the box filter used in BRIEF) used for intensity test is of size r × r , there are N = (m − r )2 such local windows.

    Each two of them can define an intensity test, so we have C2N bit features. In the original implementation of ORB, m is set to 31, generating 228,150 binary tests. After removing tests that overlap, we finally have a set of 205,590 candidate bit features. Based on a training set, ORB selects at most 256 bits according to Greedy algorithm.”

    What am getting from the official paper and from the above paragraph is that.

    We have a patch size of 31X31 and select a size of 5X5.. We will have N=(31-5)^2 = 676 possible Sub Windows.What does it mean by removing test that overlap, we get 205,590 bit Features?

    Reply ↓
    1. gillevicv Post author

      Hi,

      It means that the total possible tests (i.e. sampling pairs) is 205,590 . From that huge amount, ORB selects a subset of 256 tests.

      Does that help? let me know if you have any questions.

      Best,
      Gil

      Reply ↓
      1. Sanjaya

        Hi Gil,
        I have also same doubt as Ledig. “What does it mean by removing test that overlap,”, what does this sentence mean? I could not figure out how they got 205,590 sampling pairs out of 228150.

      2. gillevicv Post author

        Hi Sanjaya,

        I think the authors removed all sampling pairs in which at least one of the sub-windows overlaps with another sampling pair. However, I’m not sure.

        Best,
        Gil

  16. kobzili

    thank you for your help

    i have a question about pyramid

    i wish to convert you ORB to matlab code but i have a problem about feature in multiscale
    is feature reconverted in its originale location or what
    and also did the patch extracted from the reduced image or from the original
    i need somme explication about invoving scale in feature detection

    thanks

    Reply ↓
      1. Kobzili

        Please what is the mean of the same position did we reteurn to the originale position by multiplication on the correspond scale factor

  17. Nada

    Hi,
    I need to compare two images to a similar image. I applied ORB and computer the matches between image1 and image_main, and I got a vector of best matches. Similarly, compare image2 and image_main, and I got another vector. My question, how I can evaluate the result, which image is close enough to image_main. I thought of the number of matches, but this won’t work in all cases. Is there any metric to interpret the results?

    Thanks

    Reply ↓
    1. gillevicv Post author

      Hi,

      Thank you for your interest in my blog.

      Generally, this is not a simple question and many approaches exist.

      A few approaches I can suggest:
      1. If the images are natural images (and if this makes sense to your images), check if the geometry of the matches makes sense. By that I mean that the location of the matching points in the two images should be similar (or at least make some sense).

      2. A technique I really like for filtering false matches is best buddies similarity. When matching image1 and image_main, instead of taking every descriptor in image1 and finding it’s nearest neighbor, also take every descriptor in image_main and find it’s nearest neighbor in image1. Now, take only the matches where if the nearest neighbor of a descriptor d1 (from image1) is d2 (from image_main) then d1 is also the nearest neighbor of descriptor d2. That means d1 and d2 are “best buddies” because both of them are their nearest neighbors of each other.

      3. Don’t only look at the number of matches, but also on their distance (which measures their similarity).

      Hope this helps.

      Best,
      Gil

      Reply ↓
  18. Arun

    Hi,
    I was looking into the opencv implementation ORB.
    I have two questions for which I could not find any answers till now.Hope you could help :).
    in the orb.cpp file , we could see after calculating the orientation of the patch,new rotated coordinates was computed using sampling pair and angle calculated for the patch.
    I have a doubt, in boundary region there might be a patch for which after calculating the angle of the patch and subsequently calculating the coordinates ,the pixels to be selected might lie outside the frame itself. How we need to handle it in ORB?
    My second doubt is ,while calculating the centre pixel address why layer.x and layer.y has been added what are the importance of that.
    I need to implement ORB completely on embedded hardware so i need to understand the code thoroughly before I could implement the code on embedded board.

    Thanks in advance 🙂
    Arun

    Reply ↓
  19. dimtry

    how to calculate the patch size?
    in the official it says x and y run from [-r, r] I did not get it? how to calculate the r?

    Reply ↓

Leave a comment